最近中学入試が二月の勝者という番組で話題ですね。
私も時々噂を聞いているのですが
今回は開成中学の実際の入試問題が扱われたと聞きました。
その問題は以下。
今回はこいつを解説しちゃいます!!
Contents
問題
4/11=0.3636…のように分数を少数であらわし、
その小数第一位の数字を一番目の円の半径、
少数第二位の数字を二番目の円の半径
少数第三位の数字を三番目の円の半径・・・
としていきます。
ただし、単位はメートルとします。
同じように1/7を少数であらわし、
その小数第一位の数字を一番目の円の半径、
少数第二位の数字を二番目の円の半径
少数第三位の数字を三番目の円の半径・・・
としていきます。
地点Aからこの道路の道のりを2018 m進んだ地点は
左から何番目の半円上の点となるか答えなさい。
解説~実は見掛け倒しでそんなに難しくない~
見るからに長くて難しそうに見えます。
二月の勝者では”ひらめいた”や”鮮やかな解法だ”などの会話が繰り広げられたそうですが
実際はさほどひらめきも必要なく、開成中学の中ではかなり標準的な問題です。
この問題は何ステップか”見掛け倒しポイント”が含まれていて
それをいかに回避できるかが問われていると考えています。
①1/7は循環小数なのでいくら小数が無限に続いても円の半径は周期的で有限の繰り返しの形で
あらわせる
②円が問題には出てきて、円周率の計算など複雑な計算をさせられそうに見えるが実は円だから難しいということはない。
見掛け倒しポイント1 無限に続きそうで有限の数の繰り返しである小数
1/7を実際に少数表示してみましょう。
すると0.142857142857...と142857がひたすら続きます。
こいつらを一塊と見ます。
つまりこの道は以下の図が...の先に無数に連なっている道と考えることができます。
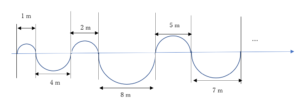
1, 4, 2, 8, 5, 7 mの半円をずっと進んだ際に何m最初から進んでいるでしょうか?
これは上の図の円を進んでいった時の右はしまでに移動する距離を表します。
(1+4+2+8+5+7)×2×3.14÷2=27×3.14=84.78 m
2018 m進むにはこの塊をいくつ進むかかんがえます。
2018は84.78×23より大きく、84.78×24より小さいので
1, 4, 2, 8, 5, 7 mの半円を23塊分通り過ぎてあと24塊まではいかない地点のどこかにいます。
周期的に半円の半径が決まっているのでこれを利用しちゃうことで2018 mなんて大きい距離も
こんな感じに扱えちゃうんです。
見掛け倒しポイントその2 円ってあまり関係ない。
先ほどの解説でみた通り、円であることは距離の演算にしか使用しないのです。
図に互い違いの半円が書いてあることで不安を覚えた小学生がたくさんいるかと思いますが
結局Aから問題文にあるように進む距離さえわかってしまえば半円であることはあまり障害になりません。
最後に解答して終わりにしましょう。
解答
1/7は小数点以下が142857で循環する。
つまり問題文で与えられている道は下記の道を一塊とした際に
これが矢印の向きに無数に連なっているものと考えることができる。

この一塊分で進む距離は(1+4+2+8+5+7)×2×3.14÷2=27×3.14=84.78 m
2018 m分進むには
2018=84.78×23+68.06よりこの一塊の最初から68.06 m進んだ地点。
(1+4+2+8+5)×2×3.14÷2=62.8より
上図において23塊分進み、さらに1, 4, 2, 8, 5 mの半円は通り過ぎてその次の半径7の円上にいることになる。
よってこの道を2018 m進むと半円は23×6+6=144個目の円周上にいる。
解答を終えて
初めて見る方は難しく見えるかと思いますが
”周期に着目する”
”そのうえで何周期目のどこにいるのか考える”
ことは中学入試に限らずどの段階の算数・数学でも大事な考えです。
しっかりこういうことを考えて問題が解けるようになってこそ
合格が勝ち取れるんだと思います。
今日はちょっと気になる方もいるのではないかなと考えて解説してみました。
それではまた!
↓この記事がよかったら拡散、twitterのフォロー励みになるのでよろしくお願いいたします!↓