どうもこんにちは！しおさいです。
今回は苦手な人も多い作図のお話です。
論理的に書けるようになろう！
実はたいていある図形の性質を用いていることをご存じでしょうか。
それはコンパスと定規が得意としている領域でできる
”ひし形”を使います。
苦手な人はぜひひし形利用できるようになって帰ってください！
Contents
作図で聞かれる内容
まずは作図で聞かれる内容です。
大体下記の内容でほとんどがひし形を用いて書ききることができます。
下のボックス内の直線のn等分以外ですね。
作図の頻出内容
・角の二等分線
・垂直
・平行
・直線のn等分
しっかり整理して覚えると早く思い出せるし便利だよ。
なぜ菱形なのか
次になぜひし形が大切なのかについて考えてみましょう。
実は必然なんです。
作図の道具でできることを考える
まずは作図の道具でできることを考えてみましょう。
作図の時に使えるアイテムは下記二つ。
①コンパス
②定規（直線を引くに限る）
コンパスを使う目的は作図問題においては円を描くことではありません。
コンパスはなぜ円を描くことができるのかまで話を深堀すると見えてきますが
コンパスができることはある点から等距離にある点の集合体をかけることにあります。
解きたかった問題に戻ってみよう
書きたかったものは下記の三点でした。
作図の頻出内容
・角の二等分線
・垂直
・平行
作図問題は書いた図形の性質を用いて解きます（教科書に載っています）
なのでどの図形が書ければ上記三点ができるか考えてみましょう。
ここで登場するのがひしがたなのです。
一回ひし形を書いてみてどこに上記三点が現れるか考えてみてください。
こんな感じに現れます。
ひし形の性質
・ひし形の対角線は互いに垂直かつ二等分になるように交わる
・ひし形の辺は互いに平行
・対角線は頂点の角度を二等分する
つまりひし形が適切に書ければ上記は全部かけることになります。
コンパスの性質と相性のいいひし形
さてここまでひし形が書ければ書きたいものが書きやすいことはわかりました。
問題はひし形が書きやすい図形かどうかです。
ひし形の定義は”四辺が等しい四角形”ですので
コンパスの”ある点から同じ長さの点の集合体をかける”という特徴と
非常に相性がいいのです。
ひし形を使う例
例えばこんな問題を考えてみましょう。
直線Lに対し並行で、点Aを通る直線を作図せよ。
解答としては下記の順番です。
①適当な点を直線L上にとる。Bとする。
②直線L上にAB=BCとなるようにCをとる
③A, Cを中心としてABを半径とする円を描く。交点をDとする。
④直線ADが求める直線。
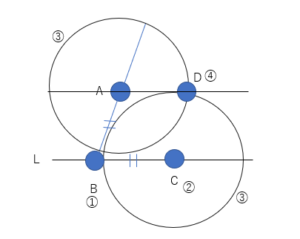
この図で四角形ABCDがひし形になっています。
平行線や垂線、角の二等分線を考えるときはどのようにひし形を書くか
こういう観点で問題を整理してみるといいかもしれません。
まとめ： 作図問題はひし形で整理
いかがでしたでしょうか。
行き当たりばったりで作図しているという声をよく聞きますが
ひし形を用いて整理するとかなりの割合のものがかけるようになります。
是非そこで空いた暗記スペースをほかの教科や自分の趣味の楽しい知識に生かしてください！
最近躓きどころやよくある疑問点の解説しています。
何か疑問などあったら何なりと聞いてみてください。
↓なぜ通分するの？
それではまた！
