こんにちはしおさいです。
今回は中学数学(高校入試範囲)もしくは中学入試(算数)で扱う
食塩水の濃度関連の問題について解説します。
この手の問題は解き方がわかっても
時間がかかることで試験の持ち時間を圧迫することが多く
早く解けないとお困りの方に届けばと思っております。
この記事を読むとわかること
・一次方程式を使った発想(中学数学)
・小学校の天秤法を使った裏技的解答(計算を短縮可能)
悩んだ際の参考にしてください!
こういう問題は中学入試問題の考え方が多いです。
小学生でも解けるけれども大人でも難しい。
そんな中学入試問題も考え方をのせています。
気になった方はこちらからどうぞ。
例題
5%の食塩水100gと8%の食塩水を混ぜたら何%になりますか。
解説
まずは基本的な定義、公式をサクっと示し、そのやり方を示したいと思います。
基本的な定義・公式
中学で濃度を考える際に知っておくべき式は以下のもののみです。
これは食塩水の濃度の定義です。
食塩水の濃度=食塩の量÷食塩水全体の重さ
両辺に食塩水全体の重さをかければ
食塩の量を求める式
食塩の量=食塩水の濃度×食塩水全体の重さ
上の式の両辺を食塩水の濃度で割れば
食塩水の重さを求める公式
食塩水の重さ=食塩の量÷食塩水の濃度
を導き出すことができます。
これで一通りの武器がそろいます。
実はこれしか使うものはないのです。
そう思って問題を解いていきましょう。
解き方~中学生の一次方程式~
基本的に中学生の一次方程式の単元ですので
そちらの方法でまずは解いていきたいと思います。
問題を見て何をしてよいのかわからないという方は
まずは問題の内容を整理することをお勧めします。
これから様々な問題に通用する考え方シリーズとして
”方針”という概念を導入したいと思います。
問題を解く方針
方針2 問題に必要な情報を整理しよう
食塩水の問題は式に出てくるのは濃度、食塩水の量、食塩の濃度の三つです。
そうなればこの三つをつかみましょう。
今回は下記のように表を使ってみます。
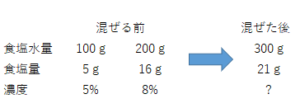
前と後に分けて書いてみるといいです。
これを見てどうしたらよいか考えましょう。
ここで一つ定石を紹介したいと思います。
定石
定石2 方程式を立てるために、等式になりそうなものを見つけよう
定石1は今回は聞かれたことは混ぜた後の食塩水濃度ですので
これをxと置きます。
すると表が次のようにアップデートできますね。
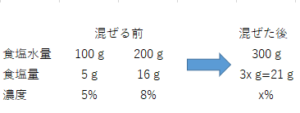
表2 文字式を置いた混ぜる前後の食塩水の関係
定石2について考えましょう。
ここが一番難しいところです。
今回注目すべきは”混ぜた前後の食塩の量は同じ”ということです。
表の中の3x=21 gですね。
これを解いて
x=7%
となります。
解き方2~実は暗算でも解ける裏技~

この問題実は天秤を使って暗算でも解けます。
まずは今回の問題を使って今回の答えを使って説明します。
混ぜる前後で食塩の量は変わらないことに着目して
100×0.05+200×0.08=300×0.07
右辺をちょっと分解します。300=100+200なので
100×0.05+200×0.08=100×0.07+200×0.07
両辺から100×0.05を引きます。
200×0.08=100(0.07-0.05)+200×0.07
両辺から200×0.07を引きます。
導きたかった式
200×(0.08-0.07)=100(0.07-0.05)
こいつ。この形が大事なんです。
このままではわかりません。
この式を
"食塩水の重さ"をおもりとみて濃度を距離する
天秤の釣り合いの式と見ます。
図にすると下記のような感じ。
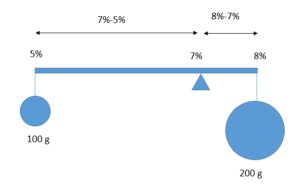
図 濃度釣り合いの天秤
この食塩水の濃度はなんと
最終的に混ぜた後の濃度の場所を支点として天秤が釣り合うのです。
これの何がおいしいかというと
方程式を立てずとも比例式で解けてしまうのです。
ここまで導くと小学生の理科の問題になります。
皆さん。小学生難しいことやってるんですよ。
できなくても決して悪くいってはいけません。
今回の問題では最初は7%がわかっていません。
求めてみましょう。
天秤において支点からの距離は
かかっているおもりの重さの逆の比になったところです。
よって視点からの距離の比は下記のように2:1になります。
すると、5%と8%の距離は3%あるのでそれを2:1に分ける点は7%ですね。
これでほぼ暗算で濃度が出てしまうんです!
終わりに
天秤を使うと方程式を解く作業と同等の作業が
暗算でできてしまうという内容でした。
この方法教科書には載っていないことが多いので
急に使うと先生に驚かれるかもしれません。
検算とか解答過程を求められない場合に使うのが
賢明かもしれませんね。
是非方程式使わなくても
サクサク解ける楽しさを味わってください。
それではまた!
